Pi; The Most Important And Mysterious Number In The World

Herbert Huffner Programming, Public Information June 29, 2021

One Of The Most Important And Famous Numbers In The Mathematical World Is The Number Pi (Π). In This Article, You Will Learn About Its Definition And Cryptic Features.

You probably remember the Pi number from the high school geometry class. The pi number is probably equally confusing for both children and adults; Because it is endless and without a pattern. However, this number is so popular that even its day is celebrated in the world.

If a foundation apparently has no application outside the world of geometry deserves praise; Why is there no celebration for any other number? This is because Pi is different from all other numbers.

It is a universal foundation that can be seen in most of the processes that take place in the world. In other words, it is the non-pattern numerical sequence that plays an important role in shaping patterns.

In fact, one of the reasons for the attractiveness and fame of the pi number is that almost everywhere we look, we see traces of it. Applications range from everyday practical questions to the world’s most complex puzzles. Join this article to learn about the mysterious and exciting dimensions of Pi.

What is Numerical Pi?

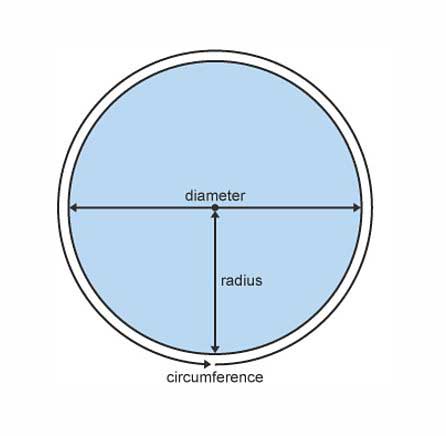
The number Pi, which symbolizes the sixteenth Greek letter π, is pronounced pi in English. In the world of geometric computing, ‌ it is the ratio of the circumference of each circle to its diameter.

π = diameter / circumference of the circle

Interestingly, it does not matter what the size of the circle is; Because this ratio will always be constant and equal to the Pi number.

You are probably familiar with the Pi number in the decimal form of 3.14, But this figure is approximate; Because pi is a “dumb” number… This means that decimal places do not end (such as 1.4, which becomes 0.25), nor are they duplicates (such as 1.6, which becomes 0.166666).

Pi number up to 18 decimal places is equal to: ‌ 3.141592653589793238.

As you can see, in this chain of 18, no digit is repeated in a row, and no fixed pattern is seen in it.

Therefore, to show the ratio of circumference to diameter, it was necessary to consider a small and approximate value such as 3.14 or 22.7. In 1706, William Jones first borrowed the Greek letter π from the Greek word for “environment” (περιφέρεια) as a number symbol; But it took about thirty years to be used as a standard constant in mathematics.

To better understand Pi, let’s do a simple experiment. Draw a circle on the paper with a compass and take a piece of yarn and place it once around the circle.

Now straighten the thread. The circumference of the circle is equal to the length of the thread.

Measure it with a ruler and write down its number. Then, measure the circle’s diameter by placing the ruler from any point on the circle to another point that intersects its center. Now, if you divide the circumference of the circle by the diameter, you get approximately 3.14.

Repeat this experiment with circles of different sizes. Each time you see, dividing the circumference of a circle by its diameter will always give an approximate number of 3.14. In other words, if you have several pieces of yarn equal to the diameter of the circle, you will need a little more than three pieces of yarn to cover the circumference of the circle.

This number is Pi; The constant ratio of the circumference of a circle to its diameter, the decimal digits of which continue indefinitely, and two duplicate numbers are never placed in a row.

Proof of the ambiguity of Pi

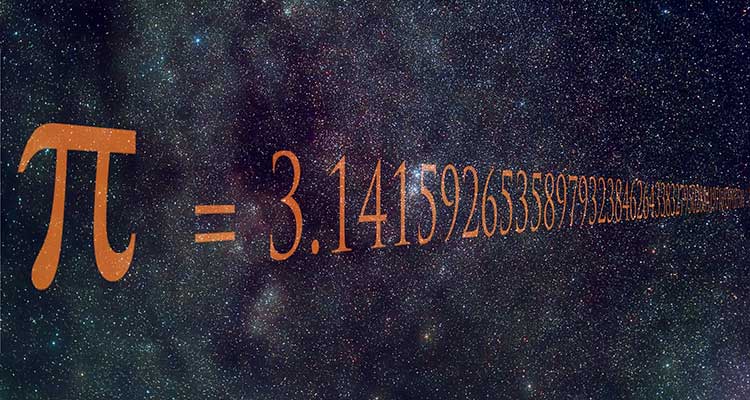
One of the wonders of the Pi number is its ambiguity; But as some people still think the earth is flat, others doubt the ambiguity of the number. You probably remember the concepts of vague numbers from school math.

Numbers such as 3, 0.5, 0.333 or -10, 1/2- or 1/7 are expressive; Because all these numbers can be written as a fraction of integers (a / b). The characteristic of rational numbers is that their decimals end somewhere (such as 222 or 1.41) or are eventually repeated from somewhere (such as 1/3, which becomes 0.3333).

In contrast, vague numbers cannot be written as fractions of integers.

Famous examples are the radical numbers 2 and the Euler number (e = 2.71828) and, of course, the same number Pi.

Although no one usually doubts the ambiguity of the radical 2, and almost everyone has accepted it as a fact in the mathematical world, there are many questions about the ambiguity of the number pi.

Is there really no end to the foundation? Is the Pi number so infinite and not repetitive that any number chain, such as your phone number, can be found somewhere?

Several equations have been proposed to prove the ambiguity of pi, the simplest of which is the proof of Niven, which assumes that numerical pi is rational; But in the end, it contradicts.

The neon method for proving the ambiguity of Pi is based on the following four steps:

1. Suppose a numerical sequence is rational; That is, π = a / b

2. Define the function f (x) as follows:

3. After the whole step, prove that if the number pi is expressed, the integral f (x) sin (x) from the values 0 to pi must be an integer.

4. Show at the same time that the integral f (x) sin (x) will be positive from 0 to pi; But the larger the value of n, the lower the zero value.

The paradox is:: If the integral answer of a number is an integer, it cannot be equal to a value between zero and one at the same time.

With these descriptions, it is proved that the initial assumption is wrong and the number is vague. In fact, if Pi is plausible, the fourth step says that the integral answer can be between zero and one; But the third step says that the answer must always be an integer. The existence of this contradiction proves that Pi cannot be expressive.

History of the Pi number

Scientists and mathematicians have realized the importance of the number pi for at least 4,000 years. In the history books following the work of Peter Beckman said, “Two thousand years BC the Babylonians and Egyptians were aware of the existence and importance of the constant π and knew the ratio of the circumference of any circle to its diameter is the same.”

Both the Babylonians and the Egyptians had an approximate value for this constant, which Archimedes later improved in ancient Greece. Finally, in the ninth century AD, the famous Iranian mathematician Mohammad Kharazmi calculated the Pi number to be four decimal places.

In the 15th century, the famous Iranian mathematician Ghiasuddin Jamshid Kashani was able to calculate 2π to sixteen decimal places; So that until 150 years later, no one could expand it any further.

In the following centuries, Chinese, Indian, and Arab mathematicians, instead of improving Archimedes’ method, increased decimal places by performing arduous calculations.

By the end of the seventeenth century, mathematical calculation methods were improving in Europe, and better formula for calculating the infinite series Pi was introduced. Isaac Newton, for example, used his binomial expansion theorem to calculate 16 decimal places quickly.

In the early twentieth century, the Indian mathematician Srinivasa Ramanujan developed incredibly efficient methods for calculating foundations later used in computer algorithms.

By the beginning of the twentieth century, about 500 foundations had been calculated. With the advancement of technology and computer computing, we now know the first digit of tens of millions of tens.

In 2019, but Haruka, development consultant cloud in Google, won with 170 terabytes of data and multidisciplinary called y-cruncher, the most accurate value of pi to calculate Universal, which includes 31. 4 trillion decimal places be. The calculation of these figures took 121 days.

It goes without saying that in 2020, the record for calculating the highest digits reached 50 trillion.

The first person to discover that the ratio of the circumference of a circle to a numerical diameter was vague was Johann Lambert, a Swiss mathematician who in 1768 showed that it was impossible to calculate the exact value of a base; Because the decimal point of this number goes on indefinitely.

In addition, the first person to decide to choose the symbol π for this vague number was William Jones, a mathematician from the United Kingdom who chose π from the Greek word meaning “environment” and introduced it in his book.

However, it took thirty years for π to become commonplace as a fixed pie. In fact, the person who made the π symbol famous was Leonard Euler, a Swiss mathematician who used the symbol in his treatise on trigonometry in the 1730s.

Integer Pi number

As mentioned, the base number is vague; That is, it cannot be expressed as a simple fraction with integers. Instead, according to mathematicians, Pi is an “infinite decimal”; the digits after the score will continue forever and do not end in any digits.

Although there is no exact value for Pi, and most calculations up to about thirty decimal places are sufficient, many mathematicians and mathematicians are still eager to calculate Pi as many digits as possible.

One of the reasons for this desire is to record and become famous. Scientists are also using it to test supercomputers and number analysis algorithms by expanding the decimal point series.

The Guinness Book of World Records for reading the largest number of Pi mentally currently belongs to Rajwir Mina Hindi, 2015. With his eyes closed, he managed to memorize 70,000 decimal places.

Some computer programmers have also been able to calculate up to 50 trillion decimal places using special algorithms. For example, pi number up to 100 decimal places is calculated as follows: ‌

3. 14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 3421

It is impossible to see the integer Pi; this number continues indefinitely, But you can see that number up to one million decimal places on piday.org.

Application of Pi number in nature

The use of Pi number can be found like optimism. In fact, wherever there is a circle in nature, such as the sun and moon disk, the double helix of DNA, the pupil of the eye, and the concentric rings formed by a body falling into the water, a number is present and used in calculations.

The pi number is also used in physics to describe waves, including light and sound. Even in the equation that examines the exact state of the universe, Heisenberg’s uncertainty principle, which states that not all quantities of an electron can be measured simultaneously, you can find the Pi.

The foot also appears in the form of rivers. Rivers that flow directly from the source to the mouth have a small meandering ratio; While rivers that flow in a spiral along the route have a higher meandering ratio.

The average meander ratio of rivers is approximately equal to Pi, and this interesting point was first explained by Albert Einstein using fluid dynamics and turbulence theory.

The π constant also led to the emergence of a new method for measuring angles (radians) that greatly helped us better understand the universe.

The pi number may not be used in our daily work. Still, it is used in most calculations related to construction, quantum physics, communication, music theory, medical surgery, air, and space travel.

In fact, NASA regularly uses the Pi number to calculate the spacecraft’s orbit. Other uses for NASA’s Pi number include determining the size of impact craters and extrasolar planets and determining the amount of propulsion for spacecraft and asteroids.

The pi number has many applications in the world of technology.

Many voice recognition software relies on the Fourier transform, which uses the number π, to capture “fingerprints” of the sound power spectrum and recognize user words.

The cell phone uses the Fourier transform to communicate with the telecommunication tower and even the human ear to detect people’s voices, which converts time or space functions into functions in terms of time or space frequency.

In addition, when we go to the radio and adjust the parameters of the electrical circuit to listen to a particular wave so that it synchronizes with the frequency of the broadcast signal, we are still dealing with the Pi number.

The pi number has many applications in modern science and is used daily in billions of calculations, including climatic simulations in massive supercomputers. Undoubtedly, with the advancement of technology, the Pi numbers will increase in the future.

World Numerical Day

In describing the importance of the number Pi, it suffices that one day it is recorded in the calendar to commemorate it. The United States has chosen March 14 (March 15) as World Pi Day, and the reason for naming this day is that in the United States, the format for writing dates is month, day, and year, and March 14 is written as 3.14, the same number as Pi. Interestingly, Albert Einstein was born the day after, and Stephen Hawking, a theoretical physicist, died on March 14, 2018.

In 1988, Larry Shaw, a physicist known as Ashna, celebrated Pi number day for the first time at the Exploratorium Science Museum in San Francisco.

By 2009, the day’s celebration was so popular that the US Congress passed a bill to formalize it, urging schools and teachers around the world to celebrate the day with fun activities and to teach students the importance of Pi and math. . In 2010, Google Doodle published a design to mark the anniversary of Pi Day.

On the opportunity to not only think about the work and efforts of mathematicians date to calculate the exact number, activities, and entertainment such as cooking and eating cake, pie, Hfzkrdn digits of Pi and watch films on the theme of pi or math (like the movie ” A Beautiful Mind,” ” P or ” Theory of Everything “).

Another pastime that can be done on this day is to write “Pai-Ko,” which is actually a mathematical version of traditional haiku poetry.

While haiku is a three-dimensional Japanese poem with a syllable pattern of 5-7-5, the poem “Pai-Ko” follows the syllable pattern of 4-1-3.

Other dates considered to commemorate the Pi number are July 22 (7/22), the approximate number Pi, and June 28 (6/28), the approximate number 2π, equivalent to 360 degrees.

Numerical Miracles Pi

The properties of the Pi number are sometimes so astonishing that some people refer to them as the “miracles” of the Pi number. Here are some of these features.

The number Pi continues indefinitely.

The number is obscure and cannot be written as a fraction of integers; For this reason, the decimal point of this number has no duplicate pattern and does not end after a digit.

In fact, the digits after the pi number count continue indefinitely. At present, up to 50 trillion pi figures have been calculated; But this is not the end of the story, and many people are still trying to break this record with the help of powerful computers.

Decimal digits are completely random.

One of the “miracles” of the pi number is that its decimal digits continue indefinitely in completely random patterns. Mathematicians have been looking for a pattern in these figures for centuries until 1768, when the Swiss-German mathematician and astronomer Johann Lambert proved that the numerical sequence is vague and that the chain of numbers has no definite pattern.

In the following, you can find any numeric string such as your phone number

Since the number is the basis of the statements and does not have a repetitive cycle, it is believed that from zero to nine can be found in every composition and string of conceivable numbers.

A set of numbers such as phone number, national code, bank card password, and any other number string you can imagine in any situation is a place in the decimal point sequence.

If you convert the letters of the alphabet to numbers (for example, based on their place number), then every text you have ever written and every book you have read so far will follow.

“It has not been proven yet,” said Patrick Ingram, a mathematician at York University in Toronto. “But in theory, if you have a string of millions, [the series of numbers you want] will eventually find a place in it and be found again indefinitely.”

To test this correctly, you can type the numeric string you want in the number search engine and see if this arrangement follows these numbers. Of course, keep in mind that this search engine only examines up to 200 million pi digits, and if your numeric string is not found in it, it probably exists in higher digits.

So far, more than 50 trillion decimal places have been calculated, and the story is still going on.

No end is defined for the foundation, But we humans have never stopped trying to figure it out. At one time, mathematicians could only calculate up to 10 decimal places; now, with the help of computer algorithms, we have been able to obtain up to 50 trillion decimal places.

In 2020, after ten months of arduous computing on his old but powerful personal computer, Timothy Mulikan was able to break the record. Timothy built the Ivy Bridge computer to calculate 50 trillion decimal places, and in 2012 used it along with 48 advanced hard drives.

To understand how amazing calculating 50 trillion numbers is, think that it would take more than 1.5 billion years to finish reading all those 50 trillion digits if you read one digit every second.

Humans can read thousands of decimal places from memory

The record for the highest number of decimal places belongs to an Indian man named Soroush Kumar Sharma, who in 2015 was able to read 70,030 digits in 17 hours and 14 minutes of memorization and topped the world rankings. Before him, another Indian man named Rajvir Mina had kept the record for 70,000 decimal places for ten years.

Akira Haraguchi, a Japanese man, claims to have lost 100,000 pi digits at a 2006 event in Tokyo; But so far, he has not registered his name in any official list.

Fortunately, you do not need to be particularly good at math to keep track of the digits.

Sharma used to be a greengrocer and passed the university engineering entrance exam.

However, he preserved all of these 70,000 digits by linking each digit to a specific image. Sharma now teaches others to strengthen memory.

In 2007, a man in the United States named Mark Omil managed to memorize 15,000 pi digits from memory. He said his way of memorizing the numbers was to read them aloud from a piece of paper and record his own voice. Then he would listen to his recordings over and over again to memorize them. He said Asperger syndrome also helped.

Even missile engineers need just over ten decimal places

Although powerful computers have calculated trillions of decimal places, we humans do not really need all of them. Even NASA engineers use up to fifteen decimal places to calculate the orbits of planets.

In fact, if you wanted to calculate the size of the observable universe, using only 39 digits in the equations would give you the answer that only the size of the hydrogen atom differed from the actual size of the universe.

In other words, there is no real calculation in the physical world that scientists would need to do to find more of these numbers.

Pi has its own language: Pilish

A special language called ” Pilish ” has been developed for the Pi number, in which the number of letters in each word is proportional to the order of the Pi digits.

blog posts