Data Recovery Is One Of The Most Important Tasks Assigned To Software Programs. In The Beginning, Databases Deal With Limited Data That Can be Check Without The Need For Special Tools, But When A Very Large Amount Of Information Is Stored In The Systems, It Is Necessary To Use Powerful Algorithms To Retrieve Information. 

Based on this, various algorithms have emerged for data recovery, and in this article, we will learn about the most important ones.

Algorithm B*

A Starless tree is a particular type of starless tree.

B, B-star, and B-plus trees are widely used in databases and file systems.

The B-star algorithm (B*) is the best-first search algorithm in a graph. This method calculates the least cost path from a node to the target node in the diagram. This algorithm was first proposed in 1979 by Hans Berliner and is related to the A* search algorithm.

A B-tree is a tree data structure that keeps data sorted and enables search, insertion, and deletion in logarithmic time. Unlike balanced binary search trees, this data structure is optimized for systems that read and write huge blocks of information. B-trees, B-star, and B-plus, are widely used in databases, file systems, data structures, and databases for indexing purposes.

Data can store in leaves or intermediate nodes in a B tree. But in the B+ tree, all data is stored in leaves, and a node can store multiple data instead of one piece of information. A B* tree is a particular type of B+ tree that is at least two-thirds of the capacity of each completion node.

Evaluation with similar trees

The main difference between the B-star tree and the B-plus tree is that in the B-plus tree, every node will have a child node when it is complete. The data in a B+ tree node is half of its capacity; This amount is two-thirds of its power in the starless tree. So the starless tree is denser compared to the pluses tree.

One of the most important differences between a binary tree and an unstarred tree is the existence of multiple data in a node in a star tree instead of one in a binary tree. Each node, along with a list of sorted data in the unstarred tree, has a pointer. It also has the next node and points out the imbalance of the starless tree.

In other search algorithms, there is no natural way to end the search for repeated searches. Also, considering the various constraints, which element should be the root is not a fixed thing. To overcome these problems, we use the starless search algorithm. The following two critical points can distinguish the B* algorithm as a simple binding-best algorithm:

First, the B* algorithm executes the support process whenever it reaches a point where its value is sufficient for our problem. At the same time, other first-best algorithms do not complete the support process until they find the final deal. There is a subtle point here: it makes no sense if we continue the movement from a node while the existing node contains a value suitable for selection. At the same time, other first-best methods do not understand this.

Second, the algorithm can choose only one of the two methods when it is on the root. It causes the continuation of the algorithm to move in a direction where the least expensive moves are determined.

X algorithm

Technically X algorithm is a recursive, non-deterministic, depth-first algorithm with backtracking. Algorithm X uses a straightforward trial-and-error approach to find all possible answers to the exact coverage problem. While Algorithm X is generally applicable as a brief description of the solution to the specific coverage problem, Knuth’s resolution may be intended to illustrate the method of the Dancing Links tool using an efficient implementation called DLX.

MTD-F algorithm

MTD-F, abbreviated as MTD(f,n) (test driver with additional memory with node n and value f), is an algorithm for minimax search that can be used as an alternative to alpha and beta pruning algorithms.

MTD-F efficiently performs zero-window, alpha- and beta-only searches with reasonable bounds (with the variable beta). In NegaScatAlpha Beta, it appears with a search space. In (AlphaBeta(root, -INFINITY, +INFINITY, depth)), the output value is between alpha and beta.

In the above algorithm, alpha-beta is wrong to find the upper or lower limits for the maximum value. Zero-window is used for more shortcuts and smaller return values. To find the total value of MTD-F, it calls alpha-beta several times to finally see the exact and final value. The precedence table returns old searches and also stores new searches to reduce re-referencing of searches.

The implementation of this algorithm has been proven to be more efficient than other search algorithms (such as Nega Scott), especially for games like chess. But in practice, this algorithm also has flaws, such as over-reliance on the precedence and delay table, search instability, and many others. Therefore, most chess game engines still use Nega Scotty, which many chess programmers consider the best chess algorithm.

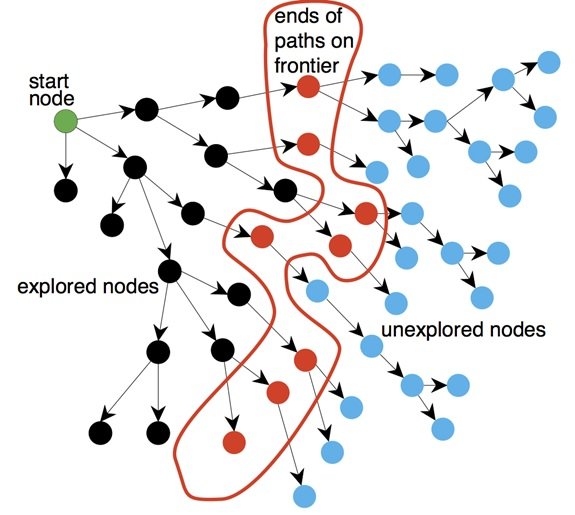
Algorithm A*

In computer science, the A* algorithm is a routing algorithm used to navigate and find a path in a graph. Due to its completeness, optimality (finding the optimal solution), and appropriate algorithm speed, it is widely used. The main problem of this algorithm is the high use of memory, which makes it perform worse than other algorithms in many practical situations.

A* is an informed search or a best-first search that starts from a given node (start node) and aims to find a path to the final node or goal with the lowest cost. This algorithm is a generalization of Dijkstra’s algorithm, which has obtained better performance in the search field using meta-heuristic methods. This method evaluates the cost of reaching node n and heuristic h(n) by combining g/n or estimating the cost of going from node n to the goal of the nodes:

F(n)=G(n)+ h(n)

Since g(n) is the cost of the path from the start node to node n and h(n) is the estimated cost of the cheapest route from n to the destination, we have:

F(n)=n cost of evaluating the most affordable solution though

So if we are looking for the cheapest solution, the first sensible thing is to try the node with the bit of h(n) + g(n). It turns out that this strategy is quite reasonable. The algorithm is optimal if Arvin’s function h(n) is acceptable and tree search. But if it is a graph search, it must be integrated in addition to being good.

If A* is used with the tree search algorithm, then its optimality analysis becomes straightforward. A* is optimal if h(n) is an admissible Arvin. That is, h(n) never overestimates the cost of reaching the goal.

These Arvins are inherently optimal because they think the cost of solving the problem is less than it is. Since g(n) accurately represents the cost of reaching n, we can immediately conclude that f(n) never overestimates the actual cost of a solution that passes through n.

A typical implementation of A* uses a priority queue to select the nodes with the lowest estimated cost at each stage to open. At each step, the node with the lowest f is removed from the queue, the function f of that node’s neighbors is updated, and the neighbors are added to the line.

The search ends when either no path from the start node to the goal is found; in other words, the queue is empty, or there are no more nodes to open.

Can do many things to improve the performance of this algorithm.

One of these tasks is how to select nodes with the exact costs from the priority queue. Suppose, in the condition of multi-node f equality, the implementation is such that the last input node is the first output node (LIFO). In that case, the algorithm works similarly to the depth-first search and avoids the search for optimal paths with the exact cost.

If apart from the minimum cost, the path itself is also in question, there must be a pointer to the node’s parent in each node so that the course can be found by following the tips after the end of the search. But should avoid, in this case, the presence of multiple instances of a node in the queue. One method is to update the parent pointer and the cost of the queued node if the node wants to be added to the line but is already in the queue instead of adding it again.

This work is not possible by the queues built based on the binary pyramid alone but can do the update with the help of the hashing table to store the node’s location in the pyramid. Also, other methods, such as using the Fibonacci pyramid to create a priority queue, can be used.

Boyer String Search Algorithm

Boyer-Moore string search algorithm is one of the practical string search algorithms published by Robert Boyer and Jay Strasser-Moore in 1977. This algorithm preprocesses the pattern string but does not preprocess the text string. And this algorithm does not check some parts of the text by using the information obtained from the preprocessing of the pattern. This algorithm is suitable when the pattern string is much shorter than the text string.

Therefore, it has a lower constant coefficient than many other algorithms. The main idea of ​​the algorithm is that instead of comparing the head of the pattern with the text, it reaches the end of the design with the text.

Boyer-Moore algorithm looks for matches of string P in string T by comparing characters in different styles. Instead of a raw search for all other games (of which there are n – m + 1), Boyer-Moore uses the preprocessing information P to check as few matches as possible.

The usual way to search for a text is to compare its characters with the first character of the pattern. When two characters are the same, the rest of the text characters are compared with the pattern characters. If there is no match, the text is rechecked, character by nature, to find a match.

Therefore, most characters of the text should check.

The critical point of this algorithm is that it does not check many text characters by comparing the end of the pattern with the text characters. Because if two characters are not the same, there is no need to check all the other characters backward.

The interesting point here is that if this character is not the same as any of the pattern characters, the next character in the text needs to be checked; n (pattern length) is the forward position.

If this character is present in the pattern, a partial transition is made to place these two characters under each other. These transitions reduce the number of characters to be checked. More precisely, the algorithm starts with the matching k = n; Therefore, the beginning of P is the same as the beginning of T.

Then the characters P and T are compared backward from the nth position. The comparison continues until either we reach the beginning of p (we found a match); Or a mismatch is observed, in which case we transfer the maximum possible amount using the rules below the template, and comparisons are made in the new model. This process continues until the pattern moves to a position after the end of T, which means there is no new match.

Hilltop algorithm

The Hilltop algorithm is used to find documents related to a specific keyword. When you enter a query or keyword in Google search engines, the Hilltop algorithm helps Google to find relevant keywords that contain more helpful information.

This algorithm is implemented on a specific index of expert documents. These are pages about a particular topic and have links to other unrelated pages related to that topic. Results are ranked based on a match.

This algorithm establishes a connection between “expert” and “authoritative” pages: a specialized page is a page to which links from many other and related documents are linked.

On the other hand, an authoritative and authoritative page is also a page that talks about a specific topic and links to many non-affiliated pages related to that topic; it is known as a reference.

A website links to expert pages becomes an authority or authority. In theory, Google will find expert pages first, and then the pages linked to them will rank well, which means that in the search engine results, priority is given to the expert page and then to the linked pages. Pages like Yahoo!, DMOZ, or academic and library sites are usually considered expert pages.