Data Structure: Familiarity With The Types Of Trees In The Data Structure
Data Structure is one of the most critical computer courses, and it has many hidden points. It is Considered a Course With High Coefficients In The Entrance Exam For Master’s Degrees in Computer Science, Doctorate, Artificial Intelligence, And Software.
In addition, at the undergraduate level, the topics described in this course are repeated in various ways in other classes. When you graduate from university and work for a software company, you must use the data structure to do most projects.
Therefore, you should not ignore any of the data structure issues and ignore them.
What should professionals be familiar with the principles of data structure?
Data structure familiarity is essential for data scientists, engineers, data mining professionals, machine learning professionals, and programmers. Software engineers have interacted with data structures in various ways for nearly half a century.
So, you must thoroughly understand data structure in data mining, machine learning, and programming. What is data organization?
Organizing data means optimizing it using a specific method based on a logical or mathematical model. Different types of data structures are used for various applications. An important point is the difference between the data structure and the algorithm.
Data structure refers to storing data on a computer for more accessible and efficient access, while an algorithm is a way to solve a problem by a computer.
Which of the following is a valuable data structure?
This question has no clear answer because each data structure issue solves a specific problem. However, some data structures are more widely used in programming projects, the most important of which are Arrays, Stacks, Queues, Linked Lists, Trees, and Graphs. ), the prefix tree (Trie), and the hash table (Hash Table). Among these, trees have a special place, which is the subject of this article.
What is a tree?
A tree is a hierarchical data structure consisting of vertices (nodes) and edges that connect them. Trees function similarly to graphs, except trees, unlike charts, do not have a cycle.
Trees are widely used in artificial intelligence and intelligent algorithms, where they provide smart solutions for storing data and solving problems effectively.
For example, all the chess games you play are tree-based. It has several trees, including the N-ary tree, the Balanced Tree, the Binary Tree, the Binary Search Tree, and the Oval Tree (AVL Tree).
He mentioned the Red-Black Tree and the 2-3 Tree. Many cyberspace users do not know about using trees in one of the most sophisticated and creative technologies we hear so much about.
Trees play a crucial role in blockchain technology. It is not harmful to know that cryptographers Stuart Haber and Scott Storrenta first attempted to build an encrypted blockchain in 1991.
They collected several documents in one block based on the hash tree. Then, they created a self-managed blockchain database using a peer-to-peer network and a distributed scheduling server.
This technology evolved gradually to see that many digital cryptocurrencies have been created based on this technology. Given the importance of trees in the digital world, we introduced the most widely used trees in this article.
2-3 Tree
Trees 2-3 are self-balancing search trees. Binary search trees may lose their balance with varying degrees of deletion.
Consider a case where you search for a binary tree and enter n data randomly sorted from small to large.
In this case, the tree becomes a linked list in which the search is of order (O (n)). In addition to losing the advantage of using the binary search tree, a large amount of memory is allocated to empty pointers.
Implementing tree insert and delete functions 2-3 ensures that the tree remains balanced during degrees and deletions. Trees 2-3 have three types of nodes called leaf nodes: nodes with only one value, nodes two, and nodes three. In node 2, X is the node’s value, L is the left subtree, and R is the right.
Each node two must have the following properties:
- Any value in L must be less than X.
- Any value in R must be greater than X.
- The path lengths from the roots to the leaves of each subtree should be the same.
In node 3, X is the node’s value, L is the left subtree, M is the middle, and R is the right. Each node three must have the following properties:
- Any value in L must be less than X.
- Any value in R must be greater than X and more petite than Y.
- Any value in R must be greater than Y.
- The path lengths from the roots to the leaves of each subtree should be the same.
It should be noted that all values are present in the leaf nodes, and the internal nodes are created only to guide the search. Each internal node is node 3 (with two or three children), whose X value equals the smallest value in the second subtree, and its Y value (if any) is similar to the smallest value in the third subtree.
figure 1
Prefix tree
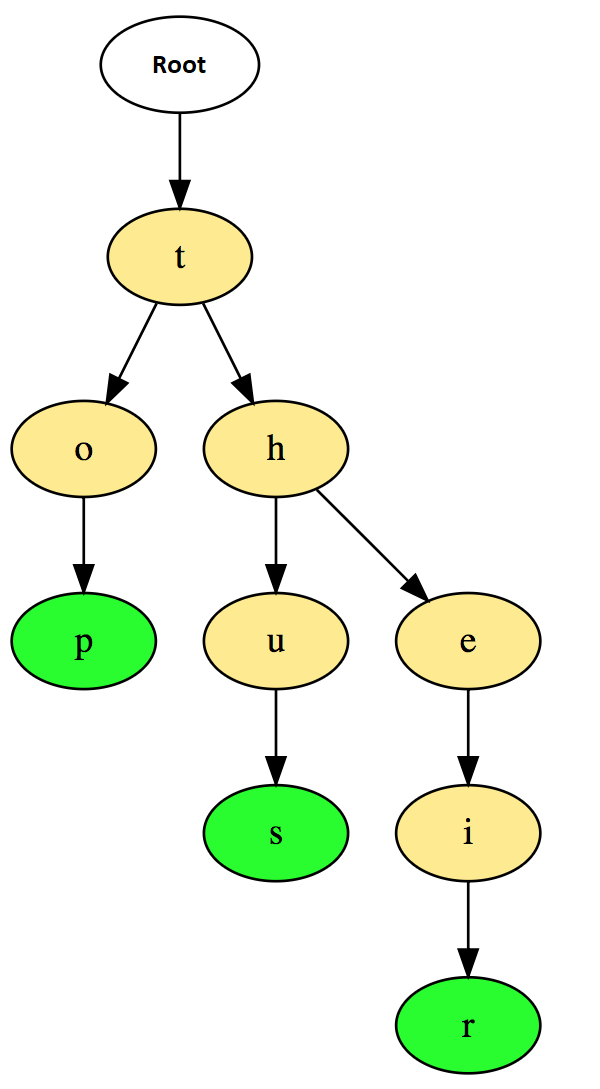
The Trie, called the Prefix Tree, is used for issues related to strings. Prefix trees allow quick retrieval and are mainly used to search for words in dictionaries, auto-suggest in search engines, and even IP routing. Figure 1 shows the function of this tree. As you can see, the terms are stored up and down in this tree.
In the figure above, the green nodes p, s, and r represent the ending letters in words top, thus, and their. Important points to note about prefix trees are how to calculate the total number of words in the prefix tree, display all the words stored in the prefix tree, sort the elements of an array using the prefix tree, format the words in a dictionary, and Build the T9 dictionary.
Extension tree
A Trie extension tree contains extensions of a given string as a key and their location in the series as a value. The suffix tree for an S string is a tree whose edges are labeled with lines so that each suffix S corresponds to a path from the tree’s root to a leaf, so this tree is a base tree for S suffixes. Building such a tree for an S string requires linear time and space regarding S length.
Once this tree is created, string operations, such as finding a subdirectory in S, finding a subdirectory with an allowable number specified for errors, finding matches for a regular expression pattern, and so on, can be done quickly.
Binary search tree
A binary search tree, sometimes called a regular binary tree, is a data structure and binary tree type. A binary tree is a data structure for storing data such as numbers. Binary Search Tree allows you to search for a number and add and remove that number faster. In addition, it will enable the implementation of dynamic collections and search tables.
The order of the nodes in the binary search tree is such that the remaining half of the tree is not examined in every comparison. Therefore, the tree search time is proportional to the logarithm of the number of numbers stored in the tree.
It is much shorter than a linear search time in an unordered array but slower than a hash operation.
A binary search tree typically consists of several nodes, each with a unique key. The tree has no duplicate keys.
All the keys in the left subtree are smaller than the root node key.
All keys in the right subtree are more significant than the root node.
The right subtree and the left subtree are binary search trees.
Self-balancing binary search tree
A self-balancing binary search tree can be any node-centric binary search tree that automatically keeps its height (maximum number of steps below the root) small when inserting and deleting the desired element.
These structures create efficient executions for immutable orderly lists and can be used as abstract data types such as associative arrays, priority queues, and collections. Self-balancing binary search trees can typically be used to build and maintain indexed directories.
The triple search tree
The triple search tree is a prefix tree, except that the nodes are in the same state as the binary search tree but have three children. Like all prefix trees, a triple search tree can be used as associative array structure data with string search capabilities. Typical uses of the triple search tree include debugging and auto-complete.
Like a binary tree where each node has a value and two pointers to its subtrees, each node of a triple search tree contains one character and three-pointers under the first, second, and third subtrees, with the letters more minor, equal child, and child.
They are known to be older. A node can point to its parent node or an index to indicate whether we have reached the end of the word. The pointer to the younger child refers to a node with a minor character than the parent.
Binary tree
A binary tree is a tree data structure in which each node has a maximum of two child nodes, the right and left children. In a binary tree, the maximum degree of each node can be two. Binary trees are used to implement binary and mass binary search trees for efficient search and sorting. A binary tree is a particular case of a k tree in which k equals 2.
Optimal binary tree
The optimal search binary tree is a type of binary search tree. If we know what elements will be inserted in the tree and see the probability that each will search, we can create a more optimal form of the binary search tree.
There are two ways to optimize a binary search tree.
One is to create a balanced search binary tree, and the other is to create an optimal search binary tree by calculating the probability of access to each element.
If the data is ready, we can search it in a binary tree to create a balanced tree. In such cases, having a balanced search binary tree, the time cost is equal to (O (LG n) in the worst case.
Cotton binary tree
In a binary tree, the number of empty connections exceeds the number of non-terminal connections. In a binary tree of the actual relationships, i.e., 2n, the number of n + 1 references is empty. These empty connections can be used to communicate with other tree nodes. The tree whose meaningless relationships are suspected in this way is called the threaded binary tree.
A binary tree can be strung in several ways depending on the tree scrolling method. The threaded binary tree allows the values in the binary tree to be scrolled through the linear scrolling method faster than the reverse scrolling of the tree as an intermediate.
In addition, it is possible to find the parent of a node in a binary tree without using parent pointers or stacks, although this is a bit slow. This feature is useful when the stack space is small or when the accumulation of parent pointers is inaccessible.
Black Red Tree
The red-black block tree is a type of self-balancing binary search tree. Rudolf Bayer first called it the symmetric B binary tree in the 1970s, but it later became known as the black rose tree.
Compared to the trees we mentioned, the black and red tree has a complex structure, yet it is swift in the worst case. To be more precise, the search, delete, and insert time for this tree is like O (log (n), where n is the number of nodes.
The main advantage of this data structure over the AVL tree is that insertion and deletion operations are performed by scrolling the tree from top to bottom only and changing the color of the nodes, making it easier to implement than the AVL tree.
A tree’s root is always black, and each node is painted in one of two colors: black or red. The leaves are black (an empty knot that has no children). It is called a black-red tree.
Who is the tree?
The KD tree organizes points in k-dimensional space and is more of a generalization of the binary search tree. This tree is a functional data structure for applications such as searches that contain multidimensional search keywords.
Each node is the next K-spot in this data structure, and each non-leaf node can be described as a separating generator that divides space into two parts.