Queueing Theory Refers To The Mathematical Study Of A Queue Or Queuing. Queue Theory Develop To Predict Queue Length And Waiting Time. 

Queueing Theory, queuing theory is recognized as a branch of operations research because results are used when deciding on the resources needed to provide services.

However, queuing theory is of great value in computer science, especially data structure, and is one of the fundamental principles of this science.

Queue theory is an important topic in analyzing systems that have a function based on input, output, and service. This theory is also important in engineering systems.

One of its important applications is the performance analysis and evaluation of computer systems that queue and service tasks in the queuing system with different inputs and outputs.

Given the importance of queuing systems in analyzing real-world problems and simulation systems in engineering sciences, familiarity with this topic is essential for computer graduates.

In queue theory, the queuing model is used to estimate the actual queuing status of the system, and therefore the queuing behavior can have a mathematical analysis. Alignment models can use symbols such as A / B / S / K / N / D, which have the following meanings:

A: Indicates the distribution of the entry time interval

B: Indicates the service time distribution

S: Indicates the number of servers

K: Indicates system capacity

N: Indicates crowd calling

D: Indicates the assumed discipline for service

In addition, the standard symbols for the distribution associated with queue theory are as follows:

M: For the Markov property (Poisson distribution, markovian distribution)

Ek: For distribution of Erlang (distribution of Erlang)

D: For Degenerate Distribution (Fixed Distribution)

G: For public distribution (Global)

Ph: For load type distribution

What are the parts of queue theory?

In queue theory, queue management is made up of the following three parts:

How to refer customers.

How to serve customers.

Customer logout conditions.

References in this regard are divided into the following two sub-categories:

Fixed: Common references between which there is a fixed time interval.

Variable: Random referral, which is more common and common,n can be seen in the bakery queue.

A simple way to maintain these two types of distributions is to distribute the time interval between references inversely and calculate the number of references per unit time based on the Poisson distribution, which is a kind of discrete probability distribution where the probability of an accident in a certain number of Indicates a fixed time or place occurring, provided that events occur at a specified average rate independent of the last time.

models

Typically, alignment models have a fixed state in the structure and display of system alignment. In this way, random models are used, the probability that the alignment system can find a specific configuration status. General procedures for structuring and analyzing alignment models include:

Specify parameters such as login rate, service time, queue capacity, and possibly queue arrangement in the system.

System status specifications: Specify general statuses such as the number of elements in the queue and…

Draw a state transfer diagram: This diagram shows the Markov chain

Because the state transfer diagram shows the steady-state, current state, and equilibrium state, we can calculate the probability of going from one adjacent state to another.

Poisson distribution

Poisson distribution is a probabilistic discrete distribution that describes an event’s probability at a certain number at a fixed time or place. These events occur at a certain average rate and are independent of the time of the last incident. In addition, the Poisson distribution use for several events at other specified distances such as distance, area, or volume.

This effect focuses more on specific random variables, such as the random variable N, which counts the number of discrete occurrences or entries that occur over a period of time—Poisson distribution in any field of use.

For example, suppose a person receives an average of four emails a day, the number of emails received on some days may be less than or more than four, but in the long run, if we monitor the receiving of emails, we see that the receiving rate is fixed.

Now suppose a process or a combination of several processes generates an event stream randomly. The Poisson distribution determines the probability that the number of these events is 2,3,4 and other numbers. The Poisson distribution predicts the degree of scatter around the average incidence rate.

Markov chain

Markov chain is a random model for describing a sequence of possible events in which the probability of each event depends only on the state of the previous event. The Markov chain is a mathematical system where the transition between your states from one state to another occurs.

The Markov chain is a memory-free random process. The conditional probability distribution of the next state depends only on the current state and is independent of its past. This memorylessness is called the Markov property. The Markov chain has many applications in real-world modeling.

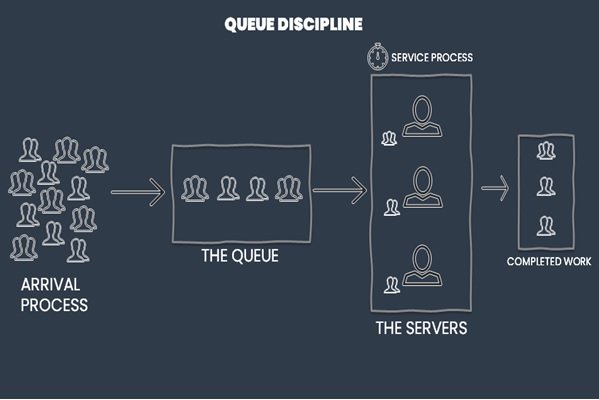
Services in queue theory

Service, or more precisely, the queue system, comprises several queues and several service providers. The most important things to pay attention to about service should be the length of the queue, the number of queues, and the order of the queue.

Queue refers to rules that specify the priority of serving waiting customers. One of the common priority rules is that the sooner you arrive, the sooner you will receive a service called First In First Out.

However, there are other rules, for example, the right to take precedence over a person who has already booked a time or service. Priority is given to the person with the emergency (in medical centers), the customers who make the most profit for the store have the right of priority, the person who has the most orders takes precedence, the person who waits for the most first or the most loyal customer takes precedence. Other rules common to queuing systems are:

Another important point to note about the queuing system and service is the queue structure.

Typically, we have four queue structure models: single-channel / single-phase, single-channel / multi-phase, multi-channel / single-phase, multi-channel / multi-phase. The simplest structure is a single channel / single phase queue.

In this case, there is only one channel for customer referral and only one phase in the service system. For example, there is an entrance door and a stand at the gas station.

Output: There are two types of outputs from customers who have received the service. Customers are either satisfied, their work is done, or they are dissatisfied and need to receive the service again.