When we think of a dynamic programming problem, we must understand the sub-problems and how they relate.

 In this article, we are going to review dynamic programming.

Algorithms and data structures are integral components of data science. However, most data scientists do not properly cover topics related to the analysis and design of algorithms during their studies. These topics are quite important, and not only data scientists but also programmers should have accurate and complete information about designing algorithms, especially dynamic programming.

In topics related to computer science and statistics, Poil planning and programming efficiently solve search and optimization problems using the two features of overlapping subproblems and optimal infrastructure.

Unlike linear programming, no standard framework exists for formulating dynamic programming problems. More specifically, the dynamic planning concept provides a general approach to solving these issues.

In each case, special mathematical equations and relations must be developed to match the conditions of the problem.

What is Dynamic Programming?

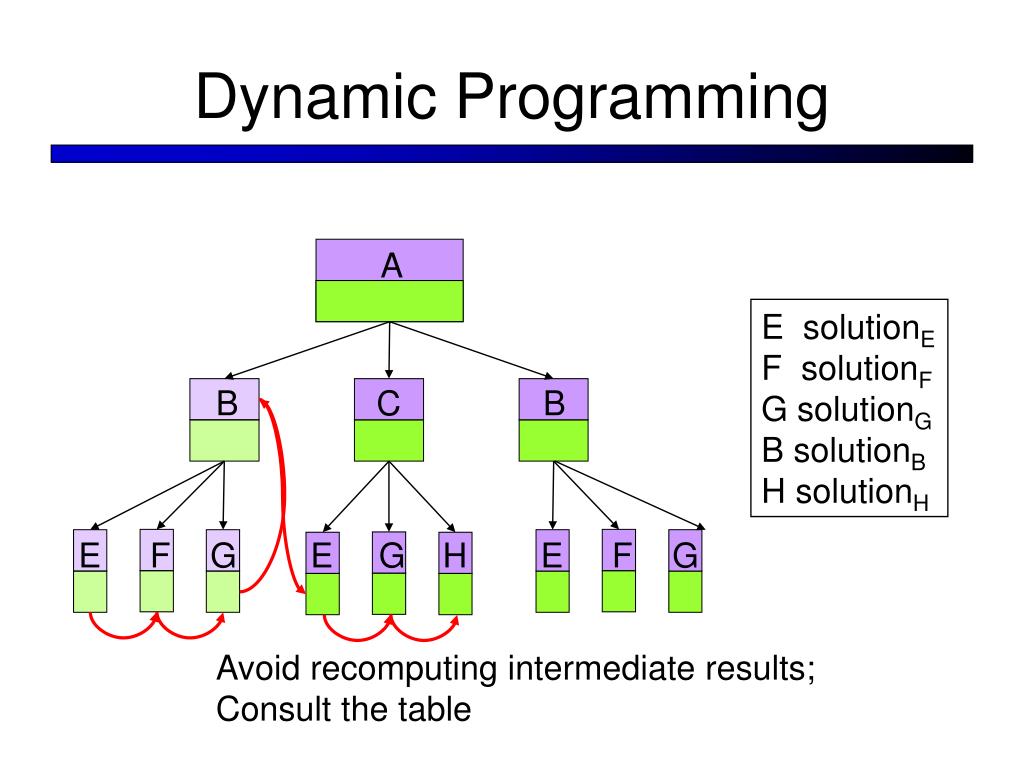
Dynamic programming often stores results in an array for reuse, and the subproblems are solved partially. In this case, the subproblems consisting of only two matrices are first calculated.

Then, the sub-problems consisting of three matrices are calculated. These sub-problems are broken down into sub-problems consisting of two matrices that have already been calculated, and the results are stored in an array.

As a result, they do not need to be recalculated. Similarly, in the next step, the subproblems are calculated with four matrices, and so on. Dynamic programming, like the division and solution method, solves problems by combining the answers to sub-problems.

The division and solution algorithm divides the problem into independent subproblems. After solving the subproblems recursively, it combines the results and obtains the answer to the main problem.

More specifically, dynamic programming can be used in cases where the subproblems are not independent, that is, when the subproblems themselves have several identical subproblems.

In this case, the division and solution method performs more calculations than the required amount by repeatedly solving the same sub-problems. A dynamic scheduling algorithm stores sub-problems once and stores their answers in a table, thus preventing sub-problems from being repeated when they need to be answered again.

What are the hallmarks of dynamic programming?

To be able to use dynamic programming for an issue, it must have two key characteristics: an optimal infrastructure and overlapping sub-problems. Solving a problem by combining the optimal answers of the overlapping sub-problems is called “division and solving.” This is why fast, integrated sorting is not known as a dynamic programming issue.

The key to dynamic programming is the principle of optimality. If the parentheses of the whole phrase are to be optimized, the parentheses of the subproblems must also be optimal. That is, the problem’s optimality requires the subproblems’ optimality.

So you can use the dynamic programming method. The optimal solution is the third step in developing a dynamic programming algorithm for optimization problems. The Development steps of such an algorithm are divided into three parts.

Not all optimization problems can be solved with dynamic programming because the principle of optimization must apply. The principle of optimality applies to a problem if an optimal solution for an instance of the situation always contains the optimal solution for all subsets.

Optimal binary search trees

A binary search tree is a binary tree of elements called a key. Each node contains a key. The keys in the left subtree of each node are less than or equal to the key in that node, and the keys in the right subtree of each node are larger. Or equal to the key of that node

Optimal infrastructure

Optimal infrastructure means that an optimization problem can be solved by combining the optimal solutions of its subproblems. Such optimal infrastructures are usually obtained with a recursive approach; For example, in the Graph (G = (V, E), the shortest path m from vertex A to vertex B shows the optimal infrastructure: Consider every middle vertex of path m.

If m is really the shortest path, then it can be considered two sub-paths, M1 from A to C and M2 from C to B, so that each of these is the shortest path between the two ends (in the same way as cutting and pasting the book Introduction to Algorithms).

The answer can be expressed recursively, just like the Belman-Ford and Floyd-Warshall algorithms.

Using the optimal infrastructure method means breaking the problem into smaller sub-problems, finding the optimal answer for each of these sub-problems, and obtaining the optimal answer to the whole problem by combining these partial optimal answers.

For example, when solving the problem of finding the shortest path from one vertex of a graph to another, we can obtain the shortest route to the destination from all adjacent vertices and use it for a general answer.

In general, problem-solving with this method includes three steps: breaking the problem into smaller parts, solving these sub-problems by breaking them backward, and using partial answers to find the general answer.

The sub-problem graph contains the same information for an issue.

Figure 1 shows the sub-problems of the Fibonacci sequences. Sub-Problem Graph A directional graph consists of one vertex for each distinct sub-problem and in the case of a directional edge from the vertex oGraph-problem x to the vertex of sub-problem y, which directly requires an optimal solution for sub-problem to determine an optimal solution for sub-problem x. y have.

For example, the subproblem graph has an edge from x to y if a top-down recursive procedure for solving x calls itself directly for solving y.

A graphubproblem graph can be considered a reduced version of the recursive tree for the top-down recursive method. In this method, we unite all the vertices of a subproblem and orient the edges from parent to child.

The bottom-up method for dynamic programming considers the outline of the subproblem in such a way that all adjacent subproblems of a subproblem are solved first.

In a dynamic bottom-up programming algorithm, we consider the outline of the subproblems to be the “topologically ordered inverse” or “inverted topologically invested subset of the problems.”

In other words, no subproblem is considered until all the subproblems it depends on have been resolved.

Similarly, the top-down (along with memorization) approach to dynamic programming can be seen as an in-depth graph search of sub-problems.

The graph size of the subproblems can help us determine the execution time of the dynamic programming algorithm. Since we solve each subproblem only once, the execution time equals the total number of times we need to solve each subproblem.
The time to calculate the answer to a subproblem is proportional to the degree of the corresponding vertex in theGraphh, and the number of subproblems is equal to the number of graph vertices.

For example, a simple function implementation Graphd the nth Fibonacci number could be as follows.

function fib (n)

if n = 0

rGraph 0

if n = 1

return 1

return fib (n – 1) + fib (n – 2)

One of the most widely used and popular methods of designing algorithms is the Dynamic Programming method.

This method works like the divide and conquer method, which is based on dividing the problem into subproblems. But there are significant differences. When a problem is divided into two or more sub-problems, two situations can occur:

The data of the subproblems have nothing in common and are entirely independent. An example is sorting arrays by the merge method or the fast method, in which the data is divided into two parts and arranged separately.

In this case, the data of one section has nothing to do with the data of the other section, and as a result, the result of that section does not affect it. The division and solution method usually works well for such problems.

The data in the sub-issue are related or shared. In this case, the so-called subproblems overlap—a clear example of such a problem is calculating the nth sentence of the Fibonacci number sequence.

Dynamic programming methods are often used for algorithms that seek to solve problems optimally.

In the method of division and domination, some smaller sub-problems may be equal, in which case the equal sub-problems are repeatedly solved several times, which is one of the method’s disadvantages.

Dynamic programming is a bottom-up method, meaning we go from solving more minor to more significant problems.

Structurally, the method of division and domination is top-down; that is, logically (not practically), the process starts from the initial problem and goes down to solve more minor issues.