In supervised learning, a machine is trained with labeled data. This means that all data is already labeled correctly. This can be compared to a student learning in the presence of a teacher.
Machine learning can be broadly divided into supervised learning and unsupervised learning in Python .
Benefits of supervised learning in Python
Using supervised learning, new data can be collected or created based on past data. Performance metrics can be optimized based on experience. Supervised learning makes it possible to solve various computational problems in real environments.
The meaning of unsupervised learning in Python
Unsupervised learning is a machine learning method in which no monitoring is done on the model. In other words, the model is allowed to analyze the data itself and categorize the information. This is done with unlabeled data. Supervised learning has the ability to perform more complex activities than supervised learning. But the results are not very predictable.
Benefits of Unsupervised Learning in Python
- Using unsupervised learning, all the unknown patterns in the data can be discovered.
- Unsupervised learning is very useful for finding features that can be used in data categorization.
- All processes take place in a real-time environment, so all data is entered into the model and labeled in the presence of learners.
- It is very easy to get unlabeled data because most of the data is generated by a computer, but labeled data requires manpower.
How unsupervised learning works
Consider an example to illustrate how unsupervised learning, consider a baby and a pet dog. This child knows his pet dog and plays with him easily. Now an acquaintance has brought another dog with him to the baby’s house and his dog intends to play with that baby.
This baby does not know the dog, but you can see familiar features in him (such as ears, standing on 4 legs, etc.) that are similar to his dog. As a result, the baby will recognize the animal as a dog.
This method is called unsupervised learning, in which nothing is taught, but conclusions are drawn from previous data.
Prepare data for unsupervised learning with Python
We use the Iris database to easily understand the subject and estimate the data. There are 150 records in this data set that have 4 properties. These characteristics include petal length, petal width, sepal length, sepal width. The Iris data set has 3 classes: Setosa, Virginica and Versicolor. In this example, we will introduce all 4 properties of our flower to the unsupervised learning algorithm, and this model will identify which class each Iris belongs to.
In this example, the Python scikit-learn library is used to load Iris data and the matplotlib is used to visualize the data.
The following code is for data exploration and data preparation:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
<span style=“font-size: 16px;”># Importing Modules
from sklearn import datasets
import matplotlib.pyplot as plt
# Loading dataset
iris_df = datasets.load_iris()
# Available methods on dataset
print(dir(iris_df))
# Features
print(iris_df.feature_names)
# Targets
print(iris_df.target)
# Target Names
print(iris_df.target_names)
label = {0: ‘red’, 1: ‘blue’, 2: ‘green’}
# Dataset Slicing
x_axis = iris_df.data[:, 0] # Sepal Length
y_axis = iris_df.data[:, 2] # Sepal Width
# Plotting
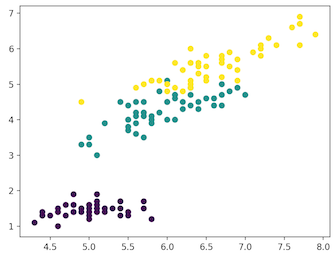
plt.scatter(x_axis, y_axis, c=iris_df.target)
plt.show()
[‘DESCR’, ‘data’, ‘feature_names’, ‘target’, ‘target_names’]
[‘sepal length (cm)’, ‘sepal width (cm)’, ‘petal length (cm)’, ‘petal width (cm)’]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]
[‘setosa’ ‘versicolor’ ‘virginica’]</span>
|
- Self: SETOSA
- Green: VERSICOLOR
- Yellow: VIRGINICA
Types of clusters
In data clustering, inputs are grouped into different groups that have the same properties.
- Right: Image of clustered data
- Left: Original data image
In the images above, the image on the left is for raw data without clustering, and the image on the right is for clustered data based on their properties. When an input is given to a model to estimate it, it finds a suitable cluster for it according to its characteristics. This is called estimating or clustering data.
K-means clustering in Python
K-means clustering is an iterative clustering algorithm that aims to find the local maximum in each iteration. At the beginning, the appropriate number of clusters is selected. In our example there are 3 classes, so we design the algorithm to divide the data into three groups. To do this we must use the n_clusters command.
We randomly place three points in three clusters. Based on the geometric center distance of the points from each other, the next inputs are categorized in their respective clusters, and each time the geometric center distance is recalculated for all clusters.
The geometric centroid of each cluster is a set of properties that define the resulting group. By examining the geometric centrifugal weight, we can understand the characteristics of each cluster.
In this example, using the scikit-learn library, we enter the K-means clustering model into the program, identify its properties, and perform the estimation operation.
Implementation of K-means clustering in Python
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
<span style=“font-size: 16px;”># Importing Modules
from sklearn import datasets
from sklearn.cluster import KMeans
# Loading dataset
iris_df = datasets.load_iris()
# Declaring Model
model = KMeans(n_clusters=3)
# Fitting Model
model.fit(iris_df.data)
# Predicitng a single input
predicted_label = model.predict([[7.2, 3.5, 0.8, 1.6]])
# Prediction on the entire data
all_predictions = model.predict(iris_df.data)
# Printing Predictions
print(predicted_label)
print(all_predictions)
[0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 1 1 1 1 2 1 1 1 1 1 1 2 2 1 1 1 1 2 1 2 1 2 1 1 2 2 1 1 1 1 1 2 1 1 1 1 2 1 1 1 2 1 1 1 2 1 1 2]</span>
|
Hierarchical clustering in Python
As the name implies, hierarchical clustering is an algorithm that categorizes clusters hierarchically. This algorithm starts with the data assigned to a cluster.
In the next step, the two clusters that are closest to each other are merged. This algorithm ends when there is only one cluster left.
The result of hierarchical clustering can be represented using a dendrogram. For example, we used the Grain database.
Implementation of hierarchical clustering
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
<span style=“font-size: 16px;”># Importing Modules
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt
import pandas as pd
# Reading the DataFrame
seeds_df = pd.read_csv(
“https://raw.githubusercontent.com/vihar/unsupervised-learning-with-python/master/seeds-less-rows.csv”)
# Remove the grain species from the DataFrame, save for later
varieties = list(seeds_df.pop(‘grain_variety’))
# Extract the measurements as a NumPy array
samples = seeds_df.values
“”“
Perform hierarchical clustering on samples using the
linkage() function with the method=’complete’ keyword argument.
Assign the result to mergings.
““”
mergings = linkage(samples, method=‘complete’)“”“
Plot a dendrogram using the dendrogram() function on mergings,
specifying the keyword arguments labels=varieties, leaf_rotation=90,
and leaf_font_size=6.
““”
dendrogram(mergings,
labels=varieties,
leaf_rotation=90,
leaf_font_size=6,
)
plt.show()
</span>
|
Clustering differences, hierarchical clustering and K-means clustering
Hierarchical clustering is not very suitable for big data, but K-means clustering is easy to estimate big data. This is due to the linear temporal complexity (O (n) in K-means clustering, while the temporal complexity of the hierarchical clustering is exponentially (O (n2).
K-means clustering performs clusters randomly. If the algorithm is run multiple times, different results will be obtained. But in hierarchical clustering the result will be the same.
The results show that K-means clustering works best when clusters are in the shape of a multidimensional sphere (such as a circle in two dimensions or a sphere in three dimensions).
Types of data clustering
Noise data cannot be used in K-means clustering, but noise data can be used directly in hierarchical clustering.
T-SNE clustering
One of the illustrated unsupervised learning methods is T-SNE clustering algorithm. This algorithm can convert multidimensional space into two or three dimensional space and visualize it. In this model, the placement of multidimensional objects in two or three dimensions is next to each other in such a way that the same points are placed next to each other and different points are placed farther apart.
Implementation of T-SNE clustering
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
<span style=“font-size: 16px;”># Importing Modules
from sklearn import datasets
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
# Loading dataset
iris_df = datasets.load_iris()
# Defining Model
model = TSNE(learning_rate=100)
# Fitting Model
transformed = model.fit_transform(iris_df.data)
# Plotting 2d t-Sne
x_axis = transformed[:, 0]
y_axis = transformed[:, 1]
plt.scatter(x_axis, y_axis, c=iris_df.target)
plt.show()</span>
|
- Self: SETOSA
- Green: VERSICOLOR
- Yellow: VIRGINICA
DBSCAN clustering
Spatial clustering based on distance density using noise data, abbreviated as DBSCAN clustering, is one of the most popular methods used as an alternative to the K-means clustering method. To work with this algorithm, we do not need to specify the required number of clusters, but we must specify two other parameters.
Although the implementation of this model uses the scikit-learn library to set the values of the eps and min_samples parameters by default, you usually need to set these parameters as well. The eps parameter represents the maximum distance between two points in a cluster. The min_samples parameter is the smallest number in a neighborhood that can be considered a cluster.
Implement DBSCAN clustering
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
<span style=“font-size: 16px;”># Importing Modules
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN
from sklearn.decomposition import PCA
# Load Dataset
iris = load_iris()
# Declaring Model
dbscan = DBSCAN()
# Fitting
dbscan.fit(iris.data)
# Transoring Using PCA
pca = PCA(n_components=2).fit(iris.data)
pca_2d = pca.transform(iris.data)
# Plot based on Class
for i in range(0, pca_2d.shape[0]):
if dbscan.labels_[i] == 0:
c1 = plt.scatter(pca_2d[i, 0], pca_2d[i, 1], c=‘r’, marker=‘+’)
elif dbscan.labels_[i] == 1:
c2 = plt.scatter(pca_2d[i, 0], pca_2d[i, 1], c=‘g’, marker=‘o’)
elif dbscan.labels_[i] == –1:
c3 = plt.scatter(pca_2d[i, 0], pca_2d[i, 1], c=‘b’, marker=‘*’)
plt.legend([c1, c2, c3], [‘Cluster 1’, ‘Cluster 2’, ‘Noise’])
plt.title(‘DBSCAN finds 2 clusters and Noise’)
plt.show()
</span>
|
Other methods of unsupervised learning in Python include:
- PCA or principal component analysis
- Diagnosis of anomalies
- Automatic
- Deep neural network
- Learning the method of Heb theory
- Contrasting Generating Neural Networks or GAN
- Self-organizing maps